电路题,零状态、零响应、全响应应该属于哪种?求完整解题过程
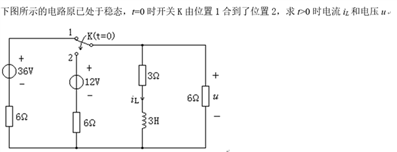
换路前,电感中有电流,电感储能,所以换路后的反应不是零状态反应;
换路后,只是外部电压变化,仍存在外部激励,所以换路后的反应也不是零输入反应;
全反应则是非零初始状态受到激励的响应,所以本题属于求解全反应。
由一阶电路微分方程可得,全反应的一般形式为 f(t) = f(∞) + [ f(0+) - f(∞) ]e^(-t/τ),
故用三要素法描述一阶电路全反应,比用经典法( 列解微分方程 )简便快捷。
本题:
换路前,电感支路两端戴维南等效电压为 18v,等效电阻为 3Ω,iL(0-) = 18/( 3 + 3 ) = 3A;
换路时,电感电流不能突变,iL(0+) = iL(0-) = 3A;
换路时,右侧6Ω电阻电流为iR,则电感支路两端电压为 6iR,电压方程为 12 - 6( 3 + iR ) = 6iR,
解得 6iR = -3v;
故电感两端电压 uL(0+) = 6iR - 3A * 3Ω = -3 - 9 = -12v;
重进稳态后,电感支路两端戴维南等效电压为 6v,等效电阻为 3Ω;
iL(∞) = 6/( 3 + 3 ) = 1A,uL(∞) = 0v;
τ = L/R = 3/( 3//3 ) = 2,-t/τ = -0.5t;
故换路后,iL(t) = 1 + ( 3 - 1 )e^(-0.5t) = 1 + 2e^(-0.5t) A;
uL(t) = 0 + ( -12 - 0 )e^(-0.5t) = -12e^(-0.5t) v;
6Ω电阻电压 u 为电感支路两端电压,
即 u = uL(t) + 3iL(t) = 3[ 1 + 2e^(-0.5t) ] - 12e^(-0.5t) = 3 - 6e^(-0.5t) v 。
下一篇:一道电路题,求解