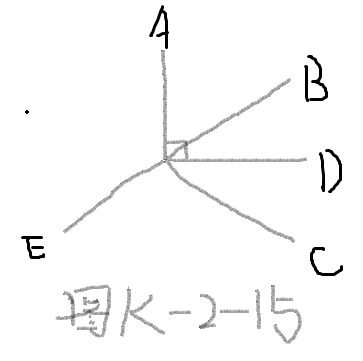
如图K-2-15,OA⊥OD，OB是∠AOD内的一条射线，OD为∠BOC的平分线，OE为BO的延长线

更新时间：2018-03-12 08:22:25 116次访问

（1）若∠AOB=60°，则∠COE=__________°

（2）若∠COE=140°，则∠AOB=__________°

（3）写出∠AOB与∠COE之间的数量关系，并说明理由。

【1】∠aob=60°，∠aod=90°

所以：∠bod=30°

有因为od平分∠boc

所以∠boc=2∠bod=60°

所以：∠coe=180-60=120°

【2】因为∠coe=140°

所以∠boc=180-140=40°

因为od平分∠boc，

所以∠bod=1/2∠boc=20°

所以∠aob=90-20=70°

【3】∠coe=2∠aob

因为∠coe=180-∠boc

=180-2∠bod

=2（90-∠bod）

=2∠aob

解 （1）∵OD平分∠BOC

        ∴∠BOC=2∠BOD=2（90º-60）=60º

      ∴∠COE=180º-60º=120º

（2）∵∠COE=140º

          ∴∠BOD=1/2（180º-140º）=1/2X40º=20º

      ∴∠AOB=90º-20º=70º

（3）∵∠BOC=2∠BOD=2（90º-∠AOB）

      又∵∠BOC=180º-∠COE

      ∴180º-∠COE=2（90º-∠AOB）=180º-2∠AOB

    则 ∠COE=2∠AOB