这道极限题怎么做
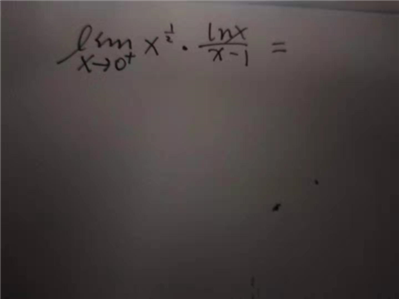
lim x→0+ x^(1/2) * lnx/( x - 1 )
= lim x→0+ lnx/ [ ( x - 1 )/x^(1/2) ]
= lim x→0+ lnx/ [ x^(1/2) - x^(-1/2) ] 分子分母为 ∞/∞ 型,用罗必塔法则
= lim x→0+ (1/x)/ [ x^(-1/2)/2 + x^(-3/2)/2 ]
= lim x→0+ 1/[ x^(1/2)/2 + x^(-1/2)/2 ]
= 1/[ 0+ + ∞ ]
= 0+
lim【x→0+】{[(x^0.5)lnx]/(x-1)}
【x→0+时,x-1极限存在;lnx/(1/√x)是∞/∞】
=lim【x→0+】[lnx/(1/√x)]/lim【x→0+】(x-1)
【∞/∞型,用罗比塔法则】
=lim【x→0+】{(1/x)/[-1/(2x√x)]}/(0-1)
=(-1)(-2)lim【x→0+】√x
=0
【附】
1/√x=x^(-1/2)
(1/√x)'=(-1/2)/(x√x)=-1/(2x√x)
热门标签: