高数级数题
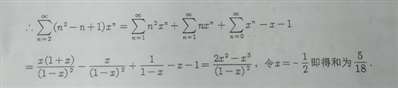这张图片前两个等号都是怎么化出来的哇
∞
∑ (n²-n-1)xⁿ
n=2
∞ ∞ ∞
=∑ n²x²- ∑ nxⁿ- ∑ xⁿ
n=2 n=2 n=2
∞ ∞ ∞
=[(∑ n²xⁿ)-x]-[(∑ nxⁿ)-x]-[(∑ xⁿ)-x-xº]
n=1 n=2 n=0
∞ ∞ ∞
=( ∑ n²xⁿ- ∑ nxⁿ- ∑ xⁿ)-(x+1)
n=1 n=1 n=0
=x(1+x)/(1-x)²-x/(1-x)²-1/(1-x)-(x+1)
【附】
∞ ∞ ∞
设 f(x)= ∑ n²xⁿ，g(x)= ∑ nxⁿ，h(x)= ∑ xⁿ，
n=1 n=1 n=0
∞
∫[f(x)/x]dx= ∑ ∫n²x^(n-1)dx=g(x)
n=1
∞
∫[g(x)/x]dx= ∑ ∫nx^(n-1)dx=h(x)-1
n=1
h(x)是首项a(1)=1，公比q=x的等比数列。
h(x)=a(1)/(1-q)=1/(1-x)
h'(x)=(-1)*(-1)/(1-x)²=1/(1-x)²
g(x)=x[h(x)-1]'=xh'(x)=x/(1-x²)
g'(x)=[x/(1-x)²]'=[(1-x)²-x*2(1-x)(-1)]/(1-x)³
=[(1-x)+2x]/(1-x)²=(1+x)/(1-x)²
∴ f(x)=xg'(x)=x(1+x)/(1-x)²
分开的3个级数分别表示为f(x),φ(x),ψ(x)
第1步看n的变化，应该直接是
原式=[f(x)-x]-[φ(x)-x]+[ψ(x)-x-1]=f(x)-φ(x)+ψ(x)-x-1(图片中可能有误,第2个级数前面为减号-）
第2步先看简单的等比数列求和
ψ(x)=1/(1-x)
从级数形式求导易得φ(x)=xψ'(x)再把ψ(x)=1/(1-x)的导数带入可得φ(x)=x/(1-x)²
同理，f(x)=xφ'(x)