分部积分法求下列定积分
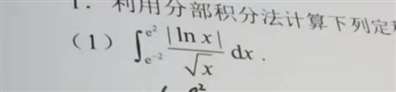
好久没碰过积分了,都快忘了.....

∫【1/e²,e²】|lnx|dx/√x
=∫【1/e²,1】|lnx|dx/√x+∫【1,e²】|lnx|dx/√x
=2∫【1/e²,1】-lnxd√x+2∫【1,e²】lnxd√x
=-2(√x)lnx+4√x【上限1,下限1/e²】+2(√x)lnx-4√x【上限e²,下限1】
=4+(2/e)ln(1/e²)-4/e+2elne²-4e+4
=8-8/e
∫lnxd√x
=(√x)lnx-∫√xdlnx
=(√x)lnx-∫dx/√x
=(√x)lnx-2√x+c
∫【1/e²,e²】|lnx|dx/√x【y=√x】
=∫【1/e,e】|lny²|d(y²)/y
=4∫【1/e,e】|lny|dy【y=e^u】
=4∫【-1,1】|u|de^u
=8∫【0,1】ude^u
=8ue^u【上限1,下限0】-8∫【0,1】e^udu
=8e-8e^u【上限1,下限0】
=8e-8(e-1)
=8
热门标签: