求边缘概率密度函数

更新时间：2022-01-18 23:22:51 160次访问

1、

fX(x) = 15x^2∫ ( x，1 )ydy = 15x^2[ y^2/2 ]( x，1 ) = 15x^2( 1/2 - x^2/2 )，0 < x < 1 ；

fY(y) = 15y∫ ( 0，y )x^2dx = 5y[ x^3 ]( 0，y ) = 5y * y^3 = 5y^4，0 < y < 1；

2、

f Y|X (y|x) = f(x，y)/fX(x) = 15x^2y/[ 15x^2( 1/2 - x^2/2 ) ] = y/( 1/2 - x^2/2 )；

计算 P{ X + Y ≤ 1 }，需要确定二重积分的积分域。

既满足联合密度函数要求，又满足P{ X + Y ≤ 1 } 要求的积分域为

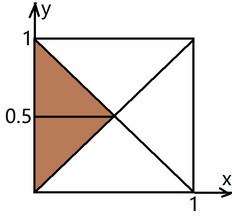
P{ X + Y ≤ 1 } = 2 * 15∫( 0，0.5 )ydy∫( 0，y )x^2dx

= 10∫( 0，0.5 )y^4dy

= 2[ y^5 ]( 0，0.5 )

= 1/16 。